
Tonight, I am going to talk about some aspects of the development of cosmology. The study of cosmology and our understanding of the universe underwent a dramatic revolution in 1915. What happened than was that a picture and the modelling of the universe passed from being what was previously essentially a branch of Art History into Science. What I mean by that was, before 1915, in the centuries before, if you wanted a universe that was square or infinite or was balanced on the back of the tower of turtles, you could have it like that - you could imagine it to be like that. If you look across the history of many different cultures around the world, you find all sorts of different world pictures: some people thought the world was cyclic, some thought it was infinite, some thought it was finite. There was no way of generating precise pictures of the universe that were in accord with all the known laws of physics. But in 1915, Einstein created a new theory of gravitation, the so-called General Theory of Relativity, and the most remarkable thing about that theory was that the equations it supplied had solutions all of which were entire universes. So by solving these equations, if you were able to, you could produce possible universes which were consistent with all the known laws of physics. So, all of a sudden, you could produce candidates for possible universes which you could go out and test against the astronomical observations.
When Einstein did this, he discovered something that, at first, was rather surprising to him: he realised that his equations were predicting that the universe was not stationary or static, as everyone had always imagined; that space was not like a theatrical stage that was fixed and had planets, stars and comets moving around on it. The equations were telling him that their possible solutions tended to be where everything changed, either expanded or contracted into a gigantic lump of mass. He did not like this idea, and he noticed that, in his equations, there was the possibility for an extra piece of the gravitational force, a piece that was not just attractive, like Newton’s old gravitational force, but an extra part that was repulsive and got stronger as things got farther and farther apart, whereas Newton’s attraction got weaker and weaker as things got farther apart. Einstein liked this force because you could balance Newton’s attraction with his new repulsive force, and that would allow the universe to be static. This was the first solution, the first type of universe that was found from Einstein’s equations, which was found by Einstein himself. This repulsive force, which we will meet later on, is sometimes called the lambda force, or, the term that created it, the cosmological constant, Λ.
In this static universe of Einstein’s the distances do not increase at all, they are just always the same. The universe has no beginning, and it has no end. So the attractive force of Newton’s laws equalled Einstein’s repulsive force, and the universe had no acceleration:
Unfortunately, rather quickly, this type of universe fell into disrepute. It is rather like having a needle which you balance on its point. Under perfectly stable conditions, it could remain balanced at that point, but the slightest disturbance, the slightest wiggle, will make it fall down. This universe has that sort of instability. With any slight movement in the universe away from perfect symmetry, it will either begin to expand or it will begin to contract. Therefore, this universe was not a viable, realistic possibility. Einstein very quickly came to appreciate this, and he called the introduction of this lambda force the biggest blunder of his life. Although, unfortunately, other people seized upon it, at the time, and found it rather interesting.
The next type of universe that was found from his equations was an expanding one, and it was found by a Dutch astronomer, Willem De Sitter. He decided to look for a type of universe where only the lambda force was present, or it was overwhelmingly bigger than Newton’s force, and this allowed a universe which expanded following an exponential trajectory. So, again, it has no beginning. You can follow it to a past eternity, it will get closer and closer to this zero, but never actually get there. And, likewise, it has no end in the future. We will see, later on, that this type of universe has turned out to be extremely important. It does not exactly describe our universe, but it plays an important role in our understanding of it.
The person who first hit the jackpot and uncovered the key types of universe that are possible from Einstein’s Theory was a meteorologist and mathematician from St Petersburg, later Leningrad, and that was Alexander Friedmann. He was one of the first atmospheric scientists, and he did a lot of experimental work, but he was a formidable mathematician – a mathematical specialist in differential equations and curve geometries – and one of the few people in the world, like De Sitter and Eddington in this country, who had the mathematical knowledge that enabled him to understand Einstein’s Theory and to go about seeking solutions of these formidable mathematical equations.
Friedmann’s atmospheric science was somewhat reckless, in that, for a long while, he held the world altitude record for ballooning. So he would go up to enormous altitudes and do things that would surely be challenged by the Health & Safety Inspectorate today! He would calculate, for example, that when he reached a particular altitude, the air would be sufficiently thin that he would become unconscious, and then the trajectory of the balloon would be pre-calculated so that he would work out that he would regain consciousness at a particular altitude on the descent. In the meantime, his instruments would have been continually making measurements, during his period of unconsciousness. So he was a serious scientist, who died, as you can see, at a only 37, in 1925. He did not die in a ballooning accident, but undoubtedly from pneumonia and illnesses brought about by repeated extreme experiences at high altitude.
What Friedmann did was to solve Einstein’s equations with and without his mysterious lambda force, and he realised that there were just two types of universe: a universe that has some apparent beginning and keeps on expanding and carries on forever; and a more claustrophobic sort of universe that expands to a maximum and then contracts back to a big crunch. In between, there is a sort of British Compromise universe, that just manages to expand fast enough to continue forever.
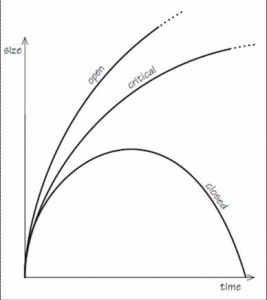
I always like to say, many years ago, I was invited by Mrs Thatcher to give a lecture on cosmology to her and some members of her Cabinet at 10 Downing Street, and because it was that sort of occasion, you had to go along a few days before and do a bit of a practice while they were putting the bullet-proof glass in the Chief Whip’s windows. So, I talked for five minutes, and showed a picture illustrating this British Compromise universe, and the Prime Minister’s Special Advisor, afterwards, said, “Oh, I thought it went very well, and I think the Prime Minister will be very interested in this. But I have just got one comment.” He said, “When you mention that British universe, try to be much more upbeat – it is just the sort of thing the Prime Minister likes to hear about!” So it was good to know the country was in such wise hands…
The interpretation of these universes is rather simple: if we think back to what happens when you want to launch a rocket into space from Cape Canaveral, there is a critical speed that you have to exceed on launch if you want to escape the Earth’s gravitational field and have your rocket go off towards the Moon or Mars or wherever you are sending it. If you do not achieve that speed, it is like throwing something into the air, where the pull of gravity will bring it back to Earth. So, in these universes, there are some that have a launch speed, as it were, less than that critical escape speed - for the Earth, it is 11km per second – and so they come back and retract. Gravitational pull is enough to overcome the energy of expansion. Other universes have more than the escape speed, and they go and expand forever. This critical universe though, between these two, is the compromise universe, which has exactly the critical speed. And, until probably about 13 years ago, this critical universe in the middle was as good a description of our universe as any.
Back then, in 1922, Friedmann had a rather awkward experience after publishing these findings. These solutions were largely ignored, it seemed, for reasons that no one could quite understand. Einstein thought that Friedmann had just done the mathematics incorrectly and there could not be any solutions like this – he thought they had to be static. Friedmann was rather shocked that Einstein thought this, but one of Friedmann’s friends from St Petersburg spent that summer in Berlin, and persuaded Einstein, rather quickly, that in fact Einstein had made a mathematical error in his analysis of these possible universes, and that these were, indeed, solutions of his equations. So Einstein quickly wrote to the journal, pressed upon it the importance to publish this paper of Friedmann’s as soon as possible, and added his own little endorsement that the paper was of importance.
So these are often called the Friedmann universes. You will notice that, if you discover a solution of Einstein’s equations that describes a universe, you tend to get it named after you. This is not always the case, but if it is a universe that has got a brand new and novel property, then it will tend to be named after you.
Meanwhile, astronomers were gradually learning to make observations that could shed some light on whether the universe really was expanding, and the famous name associated with this is of course Edwin Hubble, who has the space telescope named after him, but his co-worker, who I think did most of the technical work but rarely got any credit, was Milton Humason. When Hubble was young, he was a fine sportsman, fought a draw against the world boxing light heavyweight champion, then he became a lawyer, then he was an astronomer – that is the way you went in those days! Nobody liked him much though, because he was a terrible snob and insisted on being called “the major” at the telescope, so he was a sort of professional Englishman, even though he was American, which did not endear him to his American colleagues.
Humason was rather different. Humason left school was he was thirteen, had no formal education after that age at all, and was employed as a mule driver taking the kit up to the telescope at Mount Wilson – the photographic plates, the stores, the provisions etc. A couple of years later, he graduated to become the janitor at the telescope, looking after the men’s room, as they would call it, and so forth. And then there was an opportunity to help out over a few nights with the observing, and so he volunteered, and it was soon discovered that this was an extraordinarily talented person at the technical level, with the photography, with the optics, with the electronics, and so forth. In those days, to be an observational astronomer, you really had to be able to play with emulsions and plates as it was not computer-controlled as it is now. Now, even I can observe a telescope, but back then, you really needed all sorts of rather specific technical skills, and very good eyesight and dark vision and memory of the sky and so forth. Humason turned into really one of the most skilled observers in the world, if not the most skilled technical observer in the world. Hale, the Director of Mount Wilson, recognised this rather quickly, and offered him a permanent staff position at the telescope when he was eighteen years old, which was rather remarkable. Normally, you would get a PhD and you would have a university education before you could be a candidate for such a position, and here was someone who had never even taken an O-Level, if you like, in any subject whatsoever. But still Humason collaborated with Hubble over many years, and was the person behind many of the technical observations which led to the discovery of the expansion of the universe.
He was very unlucky not to discover the planet Pluto. He should have discovered it. He was taking plates of the solar system, but there was a flaw on the photographic plate that he was using and it did not develop the image of Pluto because it was at the precise place on the plate where the flaw fell, so he did not see it, and it was discovered by Tombaugh about ten years later.
What Humason and Hubble did was to measure the colour shifts in light from distant galaxies and to use those shifts to infer how fast the sources of the light were moving. So, just like with sound, when a motorcycle drives past your window at night, at first, the sound is coming towards you and the pitch rises, as it is coming from an approaching source, and as the motorbike goes past the pitch falls, because then the sound is coming from a receding source. If you measured the change in pitch of the sound signal, you could work out how fast the motorbike is going. The same is true with colour. If you measure the colour shift, you can figure out how fast the source of the light is receding. So Humason and Hubble were able to do that, quite accurately, and they worked out how far things were away by their apparent brightness. In the time ever since, we got so much better at seeing faint things that Hubble’s law that the speed is proportional to the distance along this straight line, has got more and more accurately mapped out. So that was the astronomical discovery that the universe was expanding.
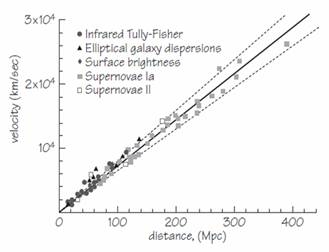
Now, to return to that in-between British Compromise universe, Einstein and De Sitter got together on their annual trips to Cal Tech in Pasadena and wrote a paper where they decided to recommend this type of universe as the simplest candidate from Einstein’s equations. It had the escape speed, it had no pressure of matter, and this lambda force was zero. If you look in correspondence to other scientists, it is rather remarkable, Einstein makes the remark, “I do not think the paper very important myself, but de Sitter was keen on it”; and then De Sitter says, “the paper by Einstein and myself I do not myself consider the result of much importance, but Einstein seemed to think it was.” Regardless this became known as the Einstein-De Sitter Universe.
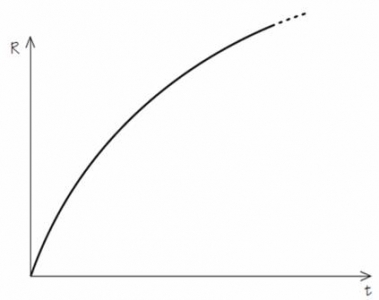
The other, and in some ways the most important, player in the game was a Catholic priest, Georges Lemaître, who graduated with degrees in Mathematics and Physics and also in Theology, at Louvain in Belgium, and then, having already served in the First World War and received the military cross, he came to Cambridge for one year as a visiting student and worked with Eddington, and then he went to America, got his PhD and returned to Europe. He discovered almost all the other types of universe that you could get, if you took Friedmann’s and you added this lambda force.
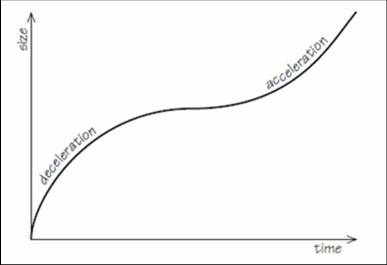
The universe that usually bears his name is one that starts expanding, rather like Friedmann’s universes, and then the lambda force starts to come into play and causes the universe to look like De Sitter’s, so it gets more and more like an exponential. So it is a universe with a change of gear: deceleration to acceleration, and we will see later on, at the end, that this is actually the best description that we have today of the universe that we observe.
When I was at the University of Sussex, one of the very famous people who died in his 95th year, Sir William McCrea, was honorary professor there. He had known all these people – he had edited Einstein’s papers and had worked with Eddington and Lemaître and De Sitter – and he always said to me that he felt Lemaître was the most sparkling and insightful person of all these great masters of the subject; that he always managed to do things in the simplest and most elegant way, with no unnecessary mathematics. Lemaître eventually became the President of the Pontifical Academy of Sciences.
There came a period of elaboration of some of these universes. Richard Tolman was the Professor of Chemistry and also Physics and Mathematics at Cal Tech. Being a chemist, Tolman was interested in things like thermodynamics and real physical processes and what would happen if you introduced them into some of these expanding universes. He first showed that you could have a sort of Far Eastern type of universe, where things are cyclic, so one of Friedmann’s closed universes but which oscillated in this way, through many never-ending sequence of cycles.
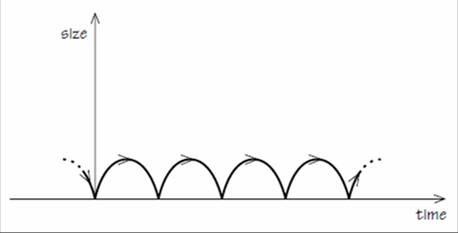
These cycles are all the same, but Tolman then realised that, if you included the second law of thermodynamics into the story, as the cycles went on, you would have more and more radiation being produced, higher and higher pressure, and each cycle would be bigger and longer than the previous one, but they would still go on forever.
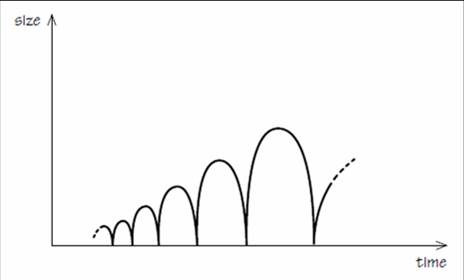
The last part of that little story was due to me and Mariusz Dabrowski, and not till the 1990s, when we noticed that, if you included that lambda force of Einstein’s in this story, then the oscillations always end. There is always a size that is reached where the lambda force takes over and no more oscillations occur, and you end up looking rather like the universe that we reside in, in fact, today.
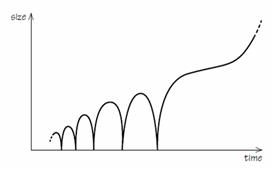
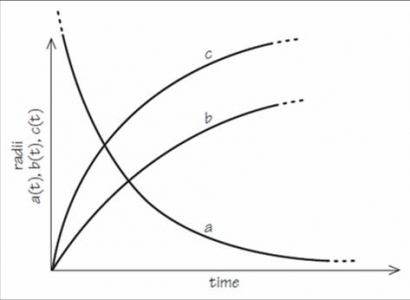
While all that was going on in Europe, there was an interesting American called Edward Kasner, who was at Barnard’s College at Columbia University in New York. He was a mathematician by training, and he was interested in studying Einstein’s equations as pieces of mathematics. He discovered a remarkable type of universe, quite different from the others: ones where the expansion did not proceed at the same rate in every direction, but had a different expansion rate in different directions. So, instead of being an expanding sphere, it is like an expanding ellipsoid. But worse than that, two directions expanded, but the third direction imploded, so in fact, rather than ellipsoid, it is like an ever-flattening pancake. But the volume, which is the product of a times b times c in the diagram below, is proportional to the time, so it is getting bigger in volume as it is getting flatter and flatter all the time. This is known as Kasner’s Universe.
Kasner gave us something else, or rather his little nine year old nephew, Sirotta, did. Kasner used to write lots of books and articles, popularising mathematics, and he invented the word googol and googolplex. A googol was 10 to the power 100, and a googolplex was 10 to the power of a googol, so 10 to the 10 to the 100. The reason that Google was used as the name for the search engine by Brin and his buddies was because they remembered this googol name for this large number that is in one of Kasner’s popular books, “Mathematics and the Imagination”. Kasner spelt it G-O-O-G-O-L, but they mistyped it when they went to see if the domain name was available, and when they found G-O-O-G-L-E was available they registered it. If they had not used that, the name they would been using for the first year of their playing with it was BackRub, so you would be back-rubbing to find things had they not changed the name to Google.
Well, this type of universe - sometimes called anisotropic, showing that it is different in different directions – led, in the years that followed, to the whole study of all the different ways that you could have universes which were different in different directions.
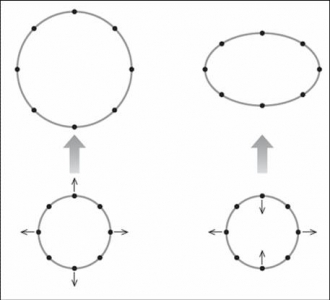
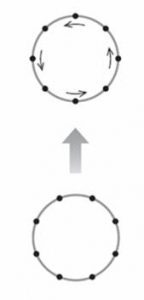
Expanding universes have an ingredient that just makes them expand, so a circular ring of particles just becomes a bigger circular ring, which is the picture on the left above. Kasner’s universe takes a circle of particles and expands them to become an ellipse of particles, so that goes out and that comes in like in the central picture above. The last thing you could do is to spin the circle of particles, so you could have a rotating universe, as in the picture on the right above. That was discovered, completely unexpectedly, in 1949, by Kurt Gödel, who was at Princeton’s Institute for Advanced Study along with Einstein.
What Gödel discovered shocked Einstein: he discovered that there could be a universe which rotated. This universe did not expand; it only rotated. So it could not describe the universe that we are in, with Hubble and Humason’s expansion, but soon other people found universes that did rotate like this and expanded as well. But the big shock which was created by the rotation was that this universe allowed time-travel to occur – time-travel into the past as well as time-travel into the future. In the universe Gödel discovered to be possible, there are closed paths in space and time, so time did not proceed by just walking in a straight line, so everyone is either in front of everyone else or behind them. It is like walking in a circle, where everybody is both behind and in front of everyone else. Such a universe can have consistent histories, where everything fits together. A typical consistent history which would be consistent factually would be for me, in Hollywood style, to return into the past, with a shotgun, and see my mother holding myself as a baby and decide I was going to shoot myself when I was a baby and thereby create a factual contradiction of history, but as I raised the gun and pointed, take aim at myself, just as I am going to pull the trigger, I feel a spasm in my shoulder, and the gun fires, the noise frightens my mother, who drops the baby, who injures his shoulder. So that is a consistent history, and the universe is safe for historians.
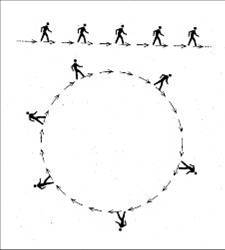
What people think about this time-travel possibility now is that it is possible. The shock for many people, from Gödel’s work, was that this was not somehow inconsistent with the laws of physics, which are all built into Einstein’s equations. There is nothing self-contradictory about time-travel into the past, but the type of universe that allows it appears to be so improbable that it is never going to create the conditions for time-travel in any bit of a universe or in the universe as a whole.
The last ingredient that was then found in this early phase of looking at universes that did things differently in different directions, was that you could have universes that were different in different places. This was something that was discovered, rather remarkably, by Newton, with extraordinary insight, more than 300 years ago, in correspondence to Richard Bentley, when Bentley was preparing his first Boyle lectures on natural theology. He had asked for Newton’s advice on all sorts of matters of gravitation and physics, and Newton pointed out that, if you had a universe where the distribution of matter was not perfectly smooth, then, as time passed, the distribution would get lumpier and lumpier and lumpier. To understand this, we can suppose that there is a distribution of points where there are some places where the average density is a bit bigger than elsewhere, and so there is a bit more gravitational pull there, and so you will pull more material to you these more massive areas than you would elsewhere. So the denser places get denser still at the expense of the sparser places, so it is a sort of gravitational Matthew principle – unto he who has more is given, and he who has not even what he has is taken away.
In 1946, a Russian physicist, who had been working somehow during the Siege of Moscow, calculating these matters, Evgeny Lifshitz, showed that exactly the same thing happens in Einstein’s Theory of General Relativity, and in the expanding universe, it just happens a bit more slowly because the expansion is working against the snowballing effect. This is a very interesting feature because it suggested to people there might be an explanation here as to why galaxies and stars exist in the universe. So if the universe begins even slightly in a non-uniform way, maybe a random amount of irregularity sprinkled around in it, what will happen, as time goes on, is those irregularities will become more and more pronounced and, eventually, they might be able to turn into things like galaxies and then into stars.
I am now going to jump forward, really to fairly modern times. I am not going to tell you everything that happened after 1946 all the way up to the 1980s because, otherwise, you would not buy my book which I am relaying to you here! There were magnetic universes, and universes where the constants of nature changed, universes with strange topologies, universes with matter and antimatter in them, and turbulent universes, so, to learn about those, you will have to read my book.
But what happened that really changed the subject in the mid-1960s was a realisation about Friedmann’s universes. If we recall his universes, what is very suggestive about those pictures is that they all have a past which was much more compressed and hot and dense than the present, and if that had been the case in our universe’s past, we ought surely to see some remnant of this hot beginning of the universe.
In 1948, George Gamow’s two students, Ralph Alpher and Bob Herman, first calculated that there should be heat radiation left over, like radiation fallout, from this hot beginning. They predicted that we should find it in the universe with a temperature of about 5 degrees above absolute zero. It was eventually found by accident in 1965, by two radio-astronomers working at the Bell Telephone Laboratories in Holmdel, New Jersey. I always think it is very impressive that when British Telecom struggles to connect my calls and get my bills right, the American television company discovers the origin of the universe!
So what Penzias and Wilson discovered, and eventually received the Nobel Prize in physics for, was this leftover radiation. Its temperature turned out to be 2.7 degrees above absolute zero, rather than the 5, but that was still very close. After that, in 1965, attention focused entirely upon these type of universes, with a hot beginning, to try and understand which of these sorts of trajectory we might be in, but most important of all, to try and understand why we might be in universes like this.
As you have seen already, there are many solutions of Einstein’s equations, many different types of universe. Can we understand that perhaps some features are inevitable? For a while, people had the idea that maybe the universe is such that, however it begins, if you wait long enough, it always ends up expanding symmetrically and slowly. Unfortunately, one of the things I did in my PhD thesis, a very long time ago, was to show this was impossible. If you wanted to turn a universe from being chaotic and irregular into the universe we see today, you had to pay for that by the production of entropy and heat, if you wanted to dissipate all those irregularities away, and that background radiation that Penzias and Wilson discovered placed a limit on how much heat could have been generated in the past in smoothing irregularity.
The most modern observations of that heat radiation has been measured by the Kobi Satellite at the end of the 1980s, when it discovered the most perfect heat spectrum ever observed in nature. When you could get above the Earth’s atmosphere and map this radiation throughout its spectrum, you found that the spectrum was almost perfectly Planck-like. If you measured the temperature of the radiation, in different directions, you found that it was the same, to within one part in a thousand. In the most modern observations, it is within one part in 100,000. So the universe is expanding symmetrically, at the same rate in every direction, to better than one part in 100,000. So the big challenge is: how do you explain this situation? Why is the universe so symmetrical? Why is it expanding tantalisingly close to that critical divide, the Einstein-De Sitter universe? And the third question: where do all those little lumps and bumps come from that Newton taught us will eventually amplify and turn into bigger lumps and bumps?
A new era in cosmology developed in about 1981, when Alan Guth, a young particle physicist, introduced what had been subsequently known as the inflationary universe, a reflection of the economic climate in 1981. This universe is a bit like Lemaître’s. It expands, like Friedmann’s, for a while, and then it changes gear, but it changes back again. So this is a universe that has this lambda force in it, but only temporarily. For a short period in its very early stages, in the first fractions of a second, it accelerates, and then it starts to decelerate again.
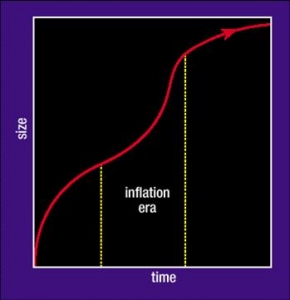
There is good reason for this picture. Back in 1981, particle physicists were finding all sorts of new types of elementary particle theory, and all of them contained a type of elementary particle and energy field that produced this effect; that when it was around in the universe, when it got produced early on, it would contribute this type of repulsive lambda force acting on its neighbours. But these particles tended to be unstable, so they would stay around for a few fleeting moments, and then they would decay into ordinary matter and radiation, and that is why it would be natural for this deceleration to be resumed. During this phase, the acceleration is going exponentially fast, and so what happens is that the universe becomes much bigger than it otherwise would have done by this time, and this little period of inflation pushes the expansion fantastically close to that critical divide of Einstein-De Sitter. If this happens, it guarantees that your universe will be close to that divide, and also, during this period, if there are any asymmetries in the expansion between one direction from another, they all get ironed out, and at the end of this period, the expansion will always be fantastically symmetrical.
If we look at our whole visible universe today and consider its 14 billion light years, as far as we can see, this surge of accelerated expansion is so rapid that it enables the whole of our visible universe today to be the expanded image of a region that is so small that light signals can pass from one side to the other and keep it very smooth and coordinated. If you did not have this accelerated expansion, our universe would be the expanded image of a region so enormously larger light could not pass from one side to the other in the past, and it would be a mystery as to why one side looked anything like the other side.
What people rapidly appreciated was that, although light signals would keep this very smooth, they would never keep it perfectly smooth. There would always be quantum fluctuations, statistical fluctuations, that have to exist in this little patch of space, and when inflation occurred, they would be stretched out and distributed around the largest scales in the universe, and ought to show up as variations in the temperature of that heat radiation from one direction to another. For the last decade, there has been two, and there is currently one ongoing European space mission that has been trying to map those temperature variations in enormous detail, to test whether this phenomenon actually occurred. The result is something like producing a temperature contour map of the whole of the universe around us, and you do a statistical analysis of how the temperature’s differences vary with separation on the sky. Here is a picture of the change in the temperature, against angular scale on the sky.
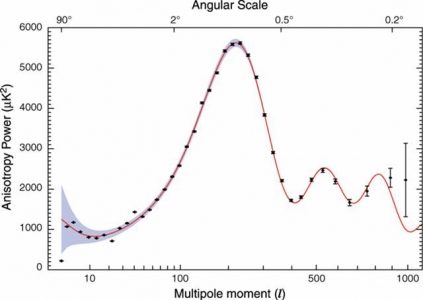
What the satellite does is to measure the temperature differences at all two degree separations, all over the sky, and then take the average, and then it measures the temperature differences for all one degree or half-degree, and so on. What you see in this picture, the solid curve is the prediction as to what should be seen if this phenomenon of inflation occurred. So the prediction was for this sudden bell-shape almost in the middle, and as you go to smaller scales, the fluctuations damp out, they get smoothed out by radiation. The solid points on the graph are the first rounds of observations. You can see that there is a remarkable agreement between what you would expect and what you see. If inflation had not occurred, you would have a picture that just had a wiggly line going across the centre. You would have no peak at the ‘bell’ point of the graph. This, then, is remarkable evidence that something like inflation happened in the past, and in the next year or two, you will see increasing amounts of data being explained in the press that really fill in this curve in fantastic detail.
It is because of this type of evidence that people take seriously the last things I will tell you about, which is the idea of universes, in the plural. So my book tells you about this succession of different types of universe that people have contemplated, but then, much more recently, it moves onto the idea that all of these types of universe, or many of them, might be co-existing, as it were, in the place that we call “the universe”. So we will now focus just on this little patch of space, which accelerated and inflated rather quickly early on, and eventually encompasses everything that we can see, what we call the visible universe.
In practice, that little patch will not be the whole universe. The universe may be infinite. There will be all sorts of other little regions outside it. You might think of this early state of the universe rather like a great foam of bubbles: there will be some sudden expansion of the bubbles, but there will be a random element, or differences from one bubble to another, some bubbles will expand a lot, some not much, and some might even expand and then implode. So what we would expect is to find ourselves inhabiting one of the bubbles which expanded and inflated enough for it to live long enough, the stars and planets to form, and for elements like carbon to be produced in the stars, so there can be astronomers and other important things. But some of the other bubbles may not have expanded by very much – there could be no stars in them, but there is no one to talk about why there are no stars in them.
There is a dramatic philosophical consequence here, that geography is predicted to be a much more complicated subject than when you were at school, that people have always been sceptical about any assumption that the universe might be the same beyond our visible horizon. You could never be sure about that, but, for the very first time, this is a positive prediction that we should not expect the universe to have a similar structure beyond our visible horizon, that if you go far enough, you should eventually encounter some of the conditions in these neighbouring bubbles, and they may not just have different temperatures and densities. In some editions of this theory, there are really radical differences, different numbers of fundamental forces of physics, even different numbers of dimensions of space that have become very large. So this is sometimes called the chaotic inflationary universe, and it takes into account the fact that statistical variations from place to place outside this bubble will also be magnified and produce very large differences.
We should not expect, tomorrow, or even next year, to run into the next bubble. That would be an extraordinary coincidence, that it just happened to be us who encountered the next bubble. It is much more probable that the amount of inflation was vastly more than was needed to smooth out our expansion, and so we will have to wait trillions and trillions of years before any evidence is found of an encounter with a part of the universe which is different to our own.
As if that was not enough, it turns out that history is more complicated than when you were at school as well, that this little patch that might have inflated to produce the whole visible universe we see today turns out to have a rather unexpected property; that it always creates within itself the conditions for further inflation of little bits of itself to occur, and this process is self-reproducing and seems to be eternal to the future. So you could think of this little region that produces these inflated patches, and then these ones creates even more, and the ones created through that create yet more. But where do we sit in this story? We are one of these patches that has had some inflationary origin, but we are just one little region in this apparently never-ending process. We have here a rather different answer to the old question, “Did the universe have a beginning?” Our little piece of it, our observable universe, on this scenario really did have a beginning, at a definite moment of time. It is not a Big Bang beginning in infinite density, but it has a beginning when that fluctuation started to inflate. But the whole process, the whole self-reproducing eternal inflationary network does not have a beginning in this scenario. The overall pattern of all the regions follows De Sitter’s universe, that first expanding one that we saw, spans exponentially, so it can be continued forever into the past perhaps and also indefinitely into the future.
An amusing piece of arithmetic, just so you get the scale of things, is that if you just focus on our little patch, you can ask, in this process, how many other universe-sized regions are proceeded as by-products and would be co-existing somewhere else today. The answer is more than 10 to the power 10 to the 77, so it is not far off a googolplex actually. This number is so large that if you were to write it out, in long-hand, so it is 1 followed by 10 to the power 77 zeros, so the observable universe is not big enough to write it down. If you do not believe me, try! In your lifetime, you could not count to a billion, just to get a scale, there is not enough time.
This type of picture of the many different regions, behaving, for all practical purposes, like separate universes, is the reason why we have words like multi-verse and concepts like multi-verse appearing in the popular press and in the scientific literature.
The very last thing I want to show you concerns the question of what the universe is like today and what is happening today, so are all bets off? Well, thirteen years ago, a striking discovery was made, that the universe is accelerating again, so it is almost as though it is starting to inflate again.
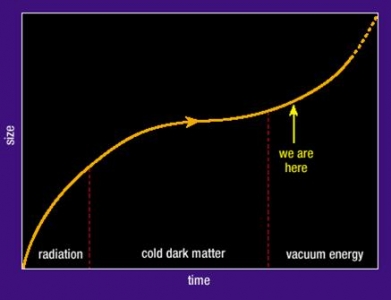
It cannot be the same process that produced inflation near its beginning, but it is more like Lemaître’s universe. You will recall that it decelerates, changes gear, accelerates. Our point on the graph is marked, where this lambda force has apparently taken over and started things accelerating again.
What is mysterious about this, the reason it could be discovered, and was discovered, only thirteen years ago, was that you needed things like the Hubble Space Telescope, to be able to extend that Hubble-Humason law to see what happened to things that are very far away. When Hubble was used to do that, it discovered that that Hubble’s law was starting to slope upwards, that the velocity of recession of the most distant things was increasing with distance. What you found, in effect, was this change of gear, this acceleration, is occurring when the universe is about three-quarters, 75% of its present extent, about 4.5 billion years ago. Coincidentally, this is not very different from when the Earth and Solar System formed, but there surely cannot be any connection. So this type of universe that we see today has this mysterious acceleration going on at the moment, it has Einstein’s infamous lambda force in it, or something that mimics it almost perfectly. So the thing that Einstein thought was his biggest blunder has turned out to be one of his biggest posthumous successes, and Lemaître’s universe describes this trajectory extraordinarily well.
However, although one can produce a beautifully accurate description of the visible universe, using that Lemaître universe model, it is really very mysterious, and the big puzzle that people have had for the last thirteen years is: why has this acceleration suddenly happened so recently? So why does this lambda quantity have the particular value that it does? If it had had a slightly bigger value, just very slightly bigger, so 10 to the -120, instead of 10 to the -121, the acceleration would have begun just a little bit earlier, too early for any stars and galaxies to form, and we would not be here. So it is absolutely crucial to understand why this begins when it does.
Until quite recently, there had never been any suggestion, no way of explaining this, but in the last half-year, Douglas Shaw and I have developed a new sort of quantum cosmology which describes what happens in universes that have a lambda term in them. Although it is another lecture, suffice it to say that this theory is able to predict, fairly precisely, why Lambda has the value that it does, and therefore why it takes over today. But more importantly, it makes another prediction, a very precise numerical prediction, that can be tested, probably in about a year’s time – data has been taken, but it takes a year to reduce it by the Planck Satellite - that a fraction, 0.0055, of the energy in the universe is wrapped up in distorting the curvature of space, and that is something you can test directly with satellite observations.
The acceleration of the universe, this lambda term that makes it run away, is sometimes called dark energy, reflecting the fact that we do not really know what it is, but we know how to describe it, and its effect is gravitationally repulsive. About 73% of the universe’s energy is made up of this lambda force and its effects. Of the rest, 4% is composed of the stuff that you and I are composed of – atoms, molecules, and what physicists see as the uninteresting stuff – and 23% is in the form of what is called dark matter. We know dark matter is there because we can see its effects. It determines how the luminous material moves around, but it is almost certainly elementary particles of a neutrino-like variety, so they interact very weakly. At the moment, there are about 400 in every cubic centimetre of space, and they are moving around at about 250km per second, so millions are going through your head at this moment and you do not feel any ill effects. So they interact just weakly, not by electromagnetic interaction, not by strong interactions, and one of the main goals of the Large Hadron Collider at CERN is to find those particles. We can calculate what their masses should be and they are heavy enough that we could not have made them before in particle physics experiments – we need the much higher energies of the Large Hadron Collider. Rather neatly, the masses where we are expecting that they will be would also guarantee that they would be the first super-symmetric particles to be discovered, but that is another goal of the LHC. So, in the next couple of years, astronomers and cosmologists are hoping that this little mystery is going to be solved by the Large Hadron Collider, that we will find the new heavy neutrino particle that we have predicted, with a mass in the range that we have predicted, to fill in this bit of the story.